안녕하세요.
이번 글에서는 제가 독학사 일반수학을 준비했던 과정과 팁에 대한 부분을 공유하려고 합니다.
독학사 1단계 일반수학 과목의 경우에는 응시자가 많지 않기 때문에 정보와 자료가 부족합니다.
그렇기 때문에 이과가 아니라면 추천을 잘 안 하지만
적어도 이 글을 찾아서 보고 계신 분이라면 어느 정도 수학에 관심이 있고
기본적으로 미적분은 하실 줄 알거라 판단됩니다.
그렇다면 저는 일반수학을 선택하는 것을 적극 추천 드립니다.
일반수학
우선 독학사 1단계 일반수학의 범위입니다.
- 집합과 함수
- 행렬과 행렬식
- 벡터
- 미분법과 그 응용
- 적분법
- 편미분법
다음은 독학사 홈페이지에서 제공하는 예시 문제입니다.
문제 하나하나씩 보면서 어떤 부분을 공부해야 하는지 짚어보겠습니다.
1번 예제 - 역함수, 미분

이 문제를 풀기 위해서는 역함수를 구하는 방법, 미분에 대한 기본적인 성질에 대해 이해하고 있어야 합니다.
기본 개념을 숙지하고 있으면 위의 풀이처럼 차근차근 문제를 풀 수 있습니다.
만약 역함수의 미분 공식을 암기한다면 바로 풀 수 있는 문제지만 굳이 그렇게까지 어렵게 생각할 필요 없이
이 문제를 통해 역함수의 개념을 다시 찾아보고, 역함수의 미분 공식도 한번 확인해 보는 정도로 학습하면 좋을 것 같습니다.
2,3번 예제 - 행렬의 성질, 행렬식, 역행렬


위의 두 문제가 2. 행렬과 행렬식 부분에서 정리해야 할 개념을 모두 포함한다고 볼 수 있습니다.
커뮤니티를 보면 독학사 일반수학에서 가장 중요한 부분이 행렬이라는 언급도 본 적이 있습니다.
그러므로 기본적으로 행렬의 성질, 행렬식과 역행렬 구하는 방법을 학습한다면 60점을 넘기는 데 큰 도움이 될 거라 생각합니다.
이 또한 너무 깊게 학습하기보다는 위의 문제를 풀 수 있을 정도만 학습하면 좋을 것 같습니다.
4번 예제 - 집합

위 문제는 집합 문제입니다.
위와 같은 문제는 벤다이어그램을 그리면 쉽게 풀 수 있지만,
집합 관련하여 집합의 포함관계, 원소의 포함관계를 공집합 개념과 섞어서 문제를 낸다면 조금 헷갈릴 수 있을 것 같습니다.
그렇기 때문에 꼭 한번은 '집합과 명제' 개념을 공집합 개념과 함께 응용하여 한번 확인하면 좋을 것 같습니다.
따라서 집합에서는 합집합, 교집합, 여집합, 차집합, 부분집합, 공집합 등의 개념을 위주로 공부하는 것을 추천합니다.
5번 예제 - 적분
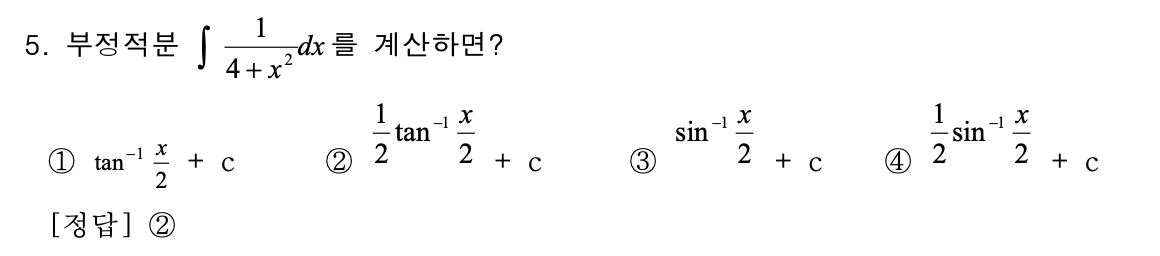
이 문제는 역삼각함수의 미분을 활용한 부정적분 문제입니다.
독학사 시험의 문제점이 이런 부분에 있습니다.
더구나 시험에 대한 정보도 부족한데 이런 문제를 예시 문제로 보여주니...
어느 수준으로 시험을 대비 해야 할지 감이 잡히질 않았습니다.
시험을 친 입장에서 말하자면 이런 문제는 25문제 중에 2~3문제 포함되어 있고
이러한 문제는 과감하게 포기하는 것이 효율적이라고 생각합니다. (60점이 목표이기 때문에)
따라서 적분의 경우에는 기본적인 적분의 성질과 정적분, 부정적분 계산 방법 정도를 학습하고 가시는 게 좋을 것 같습니다.
+풀이
https://www.youtube.com/watch?v=zX5SSWTWv5U
6,7번 예제 - 미분

6번 문제는 미분과 적분의 관계에 관한 문제이고, 7번은 미분의 정의에 관한 문제입니다.
이 정도가 딱 독학사 1단계 일반수학의 미분법, 적분법 문제의 수준이라고 판단됩니다.
그뿐만 아니라 전체적인 일반수학 문제 수준이 딱 이 정도인 것 같습니다.
두 문제를 통해 미분의 정의와 미분과 적분의 관계에 대해 한번 정리해보면 좋을 것 같습니다.
8번 예제 - 벡터

8번 문제는 세 점이 한 직선상에 있을 조건입니다.
벡터 부분에서는 이 문제처럼 특정 조건에서 값이나 식을 구하는 문제들이 주로 출제되는 것 같습니다.
1) 특정 조건하에 점의 좌표 구하기
2) 특정 조건하에 직선의 방정식 구하기
3) 특정 조건하에 평면의 방정식 구하기
따라서 내적, 외적 개념을 정리하고 위 세 가지 케이스 문제 풀이법을 학습한다면
벡터 문제도 충분히 맞힐 수 있을 거라 생각합니다.
9번 예제 - 극한값

마지막 예시 문제는 극한값 문제입니다.
사실 이 문제는 자연상수 e에 대한 정의이기 때문에 더 이상 설명할 내용이 없습니다.
극한값은 미분법의 베이스가 되는 부분인데 기본적으로 0/0 꼴, ∞/∞ 꼴 극한계산, 로피탈 정리 정도를 숙지하고 가시면 좋을 것 같습니다.
위의 독학학위제 홈페이지에서 제공하는 독학사 1단계 일반수학 예시문제 9문제를 통해서 대부분의 개념을 확인할 수 있을 거라고 생각합니다. 그리고 위에서 설명한 부분을 정리하고 학습한다면 무난하게 60점은 넘을 수 있다고 생각합니다. 위 9문제에서 언급이 안 된 내용은 편미분 정도가 있는데 편미분은 미분법을 학습하면서 기본문제 몇 문제만 풀어보는 정도로 너무 부담스럽지 않게 학습하면 좋을 것 같습니다.
궁금하신 점이 있다면 댓글로 남겨주시면 답변드리겠습니다!
'학위 취득 > 독학사(독학학위제)' 카테고리의 다른 글
| [독학사] 1단계 교양 과목 시험결과 (0) | 2022.03.21 |
|---|---|
| [독학사] 1단계 교양 시험 난이도 및 공부방법4 - 기초통계학 (2) | 2022.03.14 |
| [독학사] 1단계 교양 시험 난이도 및 공부방법2 - 국사, 영어 (4) | 2022.03.02 |
| [독학사] 1단계 교양 시험 난이도 및 공부방법1 - 국어 (0) | 2022.03.01 |
| [독학사(독학학위제)] 학습방법에 대해 공유하려고 합니다. (0) | 2022.02.28 |
